后置处理中RTCP的应用(经典干货)

2021-03-0315:08

前言

后置处理在数控加工中一直扮演着重要的角色。其定义是相对前置处理来说的。

在数控编程中，一般将定义零件模型到生成刀具轨迹的过程称为前置处理。

对于不同的工件和不同的加工工艺，前置处理是通用的。

但是前置处理不考虑机床的机械结构形式和不同数控系统指令格式之间的差别。

要想在特定的数控机床上进行加工，还需要将前置处理得到的刀位文件转换成指定数控机床能执行的数控加工程序，这一过程一般称为后置处理。

对于三坐标数控机床来说后置处理更多的关注如何生成对应数控系统的指令代码。而对五坐标数控机床，在兼顾指令代码格式的情况下，更重要的是进行运动坐标的变换。本文研究的内容主要针对五坐标数控机床的后置处理。

本文是对五坐标后置处理中的跨象限问题进行研究。所谓跨象限问题是指五坐标加工中刀轴矢量在不同象限之间来回跨越，导致五坐标机床旋转轴不断的大范围变化。从而对工件的加工过程产生潜在的威胁( 本文将在节 1对这一现 象进行详细的介绍 )。针对这一现象。本文提出利用软 RTCP功能解决跨象限问题，从而为五坐标数控机床的后置处理打下了坚实的基础。

1：后置处理中的跨象限问题；

为了介绍 RTCP功能在后置处理中的应用, 首先 要介绍五坐标后置处理中的跨象限问题。

由于五坐标数控机床的机械结构形式多种多样, 为了叙述方便, 本文以旋转轴为 B、C 轴的数控机床为 研究对象, 并且旋转轴是附加在工件上的。对于其它 形式的数控机床, 其原理与本文列举的机床类似。

转台转动的 B、C 轴形式的五坐标 数控机床后置处理的原理图如图 1所示。

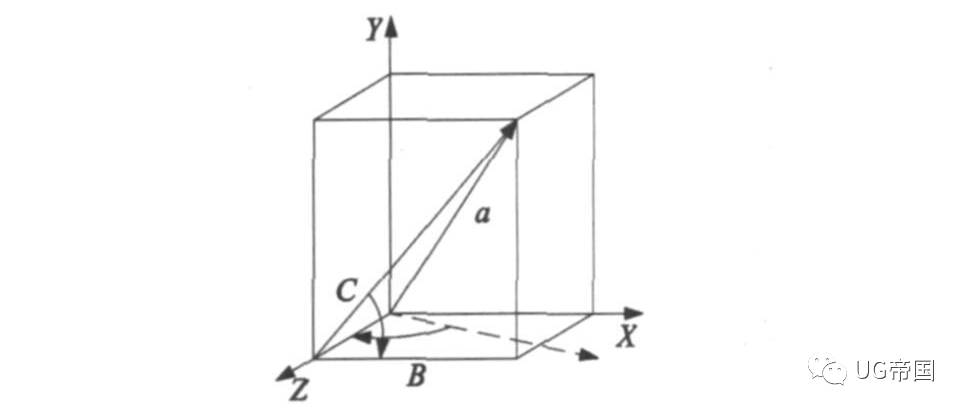
图 1 中向量 a 代表五坐标加工中的刀轴矢量, 后置处理的原理是设法将向量 a 绕坐标轴旋转到与 Z 轴重合的位置, 从而得到旋转角度 B、C, 在利用绕 指定旋转轴的坐标变换公式, 从而最终推导出后置 处理公式。

对于 B、C 旋转轴的数控机床来说, 要想将向量 a 旋转到与 Z 轴重合, 首先应将向量 a绕 Z 轴旋转 C 角, 再绕 Y 轴旋转 B 角。观察图 1, B 角的计算公式为:

式中, i、j和 k 代表刀轴矢量在 X、Y 和 Z 轴方向上的 分量。C 角的计算公式为:

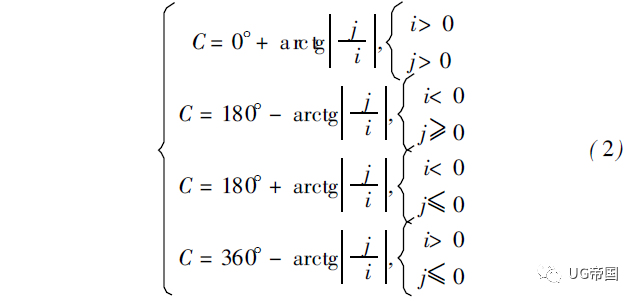
又令绕 Z 轴的旋转 C 的坐标变换公式为:

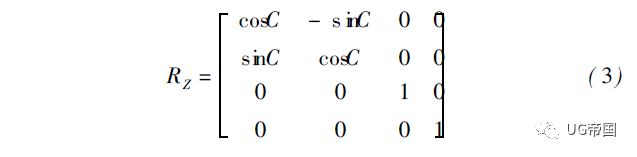
绕 Y轴旋转 B 角的坐标变换公式为:

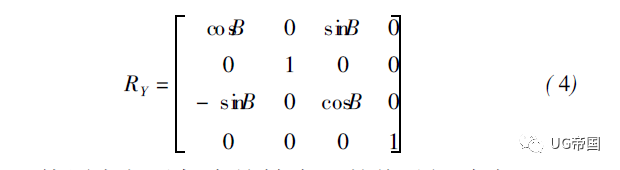
工件原点相对机床旋转中心的偏移矩阵为:

式中, g、h 和k 分别代表X、Y和Z 轴方向的偏移值。利用式( 1)、( 2)、( 3)、( 4)和( 5),可以得到BC 旋转轴的五坐标数控机床后置处理公式为:

式中, XW、YW  和 ZW   分别代表工件坐标系下刀尖点的X、Y 和 Z 坐标值。

虽然式 ( 6)得到了后置处理的计算公式, 可是在 实际的工程应用中单纯应用这个公式, 并不能完全的解决所有问题。